Porte de la rue Gargoulleau
L’architecture, miroir de l’harmonie universelle
 |
Description et historique
| Le rayonnement de « la famille platonicienne »
Pour les architectes de la Renaissance le système de rapports qui s’impose à eux, inspiré de Vitruve, doit refléter les proportions du corps humain qui créé à l’image de Dieu exprime l’ordre cosmique. Ces rapports mathématiques qui règlent l’harmonie du monde Pythagore et Platon en livrent le principe, principe non ignoré de l’époque médiévale mais auquel les humanistes comme Alberti, Politien, Landino, Pic de la Mirandole, Ficin, et d’autres membres de l’académie florentine, vont insuffler une nouvelle vigueur qui témoigne de la profonde influence du platonisme (1). Ils nous livrent de précieuses indications sur la valeur symbolique des proportions, du corps humain notamment, comme références de l’harmonie universelle, des propriétés aussi bien arithmétiques que géométriques caractéristiques de l’ Anima Mundi, de cette âme du Monde que décrit Platon dans le Timée. Platon (env. -427, -347), élève des Pythagoriciens qui voient dans le nombre le principe de toute chose, décrit dans le Timée (section 27-69) la naissance de l’univers (cosmogonie), sa structure et sa composition (cosmologie). L’univers, le cosmos (éthymologiquement : « ordre ») qui s’oppose au chaos est un tout organisé dont l’harmonie est réglée sur le principe de la proportion. L’univers se compose d’un corps et d’une âme. Le corps du monde fut créé par le Démiurge par la mise en proportion de quatre éléments : il prit d’abord du feu (sans lequel rien n’est visible) et de la terre (sans laquelle rien n’est solide) et pour les unir dans une proportion (2), il prit deux moyens termes, l’air et le l’eau, de telle façon que ce que le feu est à l’air, l’air le soit à l’eau et que ce que l’air est à l’eau, l’eau le soit à la terre (feu/air/eau/terre). L’âme du monde C’est surtout dans sa description de l’âme du monde que le philosophe montre sa maîtrise des proportions. Avant même que de former le corps nous dit-il, le Démiurge place au centre de l’univers l’âme afin qu’elle s’étende partout et englobe le corps lui-même. Pour la créer il combine trois éléments : « la substance indivisible qui se comporte toujours d’une manière invariable », « la substance divisible qui est dans le corps « , les deux liées par une troisième, « sorte de substance intermédiaire comprenant et la nature du Même et celle de l’Autre », combinaison qu’il partage ainsi : « En premier lieu, il a séparé du mélange total une portion. Ensuite il a pris une seconde portion double de celle-là ; puis une troisième portion égale à une fois et demie la seconde et à trois fois la première ; une quatrième double de la seconde ; une cinquième triple de la troisième ; une sixième égale à huit fois la première ; une septième égale à vingt-sept fois la première. Après cela, il a comblé les intervalles doubles et triples, détachant encore des portions du mélange primitif et les disposant entre ces parties-là, de telle sorte que, dans chaque intervalle, il y eût deux médietés. La première surpasse les extrêmes ou est surpassée par eux d’une même fraction de chacun d’eux. La seconde surpasse les extrêmes d’une quantité égale à celle dont elle est elle-même surpassée. De ces relations naissent dans les intervalles ci-dessus désignés, des intervalles nouveaux de un plus un demi, un plus un tiers, un plus un huitième. A l’aide de l’intervalle de un plus un huitième, le Dieu a comblé tous les intervalles de un plus un tiers, laissant subsister de chacun d’eux une fraction telle que l’intervalle restant fût défini par le rapport du nombre deux cent cinquante-six au nombre deux cent quarante-trois. Et ainsi, le mélange dans lequel il avait coupé ces parties se trouva employé tout entier .«
Francesco Giorgi : San Francesco Della Vigna, la preuve par neuf La conception albertienne des proportions et l’interprétation mathématique de l’espace, d’inspiration platonicienne, furent-elles vraiment mise en pratique ? La fameuse expression d’Alberti, glissée dans ses recommandations à Matteo di Pasti, chargé du chantier de San Francesco à Rimini, « de peur que toute cette musique ne se désaccorde » (4) atteste bien que l’intérêt du » prince architecte » pour les consonances musico-spatiales n’était pas purement théorique. Avec le mémoire rédigé par Francesco Giorgi (5) pour l’église San Francesco Della Vigna à Venise , Rudolf Wittkower nous livre la preuve que cette conception albertienne et néo-platonicienne des rapports engendrés fut bien appliquée à l’architecture à la Renaissance. San Francesco della Vigna, façade de Palladio Francesco Giorgi, moine franciscain, auteur de » De Harmonia Mundi totius « , publié en 1525 à Venise, est chargé par le Doge, en tant qu’expert, de proposer des solutions pour les proportions du plan de l’église dont la construction vient juste de commencer. Le plan initial, de Jacopo Sansovino est en effet contesté pour raison esthétique. » Sans rien altérer de ce qui a déjà été réalisé « , Giorgi va faire une suite de propositions qui recevront l’aval de trois personnalités exceptionnelles : Titien, le peintre, Serlio, l’architecte, et Fortunio Spira un humaniste très en vue, preuve supplémentaire que cette théorie des proportions ne se limite pas au seul domaine de l’architecture mais participe bien d’une esthétique globale humaniste. dans les mêmes rapports… » La « cappella grande » sera d’une largeur de 6 pas pour une longueur de 9 pas, soit un diapente, les ailes du transept seront aussi de 6 pas de large. La cappella grande, ajoutée à la nef donne une proportion quadruple ou bisdiapason ( ou double diapason) 9/18/36, et le choeur participe à cette harmonie en recevant une même longueur de 9 pas (proportion quintuple 9/27/45). La largeur des chapelles latérales sera de 3 pas, leur profondeur de 4 pas (soit 3/4, un diatessaron), la largeur des chapelles, celle du transept et celle de la nef formeront alors un diapason diapente ou une triple (3/6/9). les hauteurs de la nef et des chapelles devront suivre les mêmes règles harmoniques (ex : 12 pas pour la hauteur de la nef soit un diatessaron avec sa largeur, 9/12). Quant à la façade (élevée par Palladio à partir de 1562) Giorgi recommande qu’elle » corresponde à l’intérieur de l’église, et qu’à partir d’elle on puisse saisir la forme de l’église et toutes ses proportions « . Ces recommandations ont bien été suivies par les bâtisseurs puisque le plan actuel suit précisément ce jeu de rapports et de proportions comme le montre le schéma suivant.
Porte de la rue Gargoulleau |
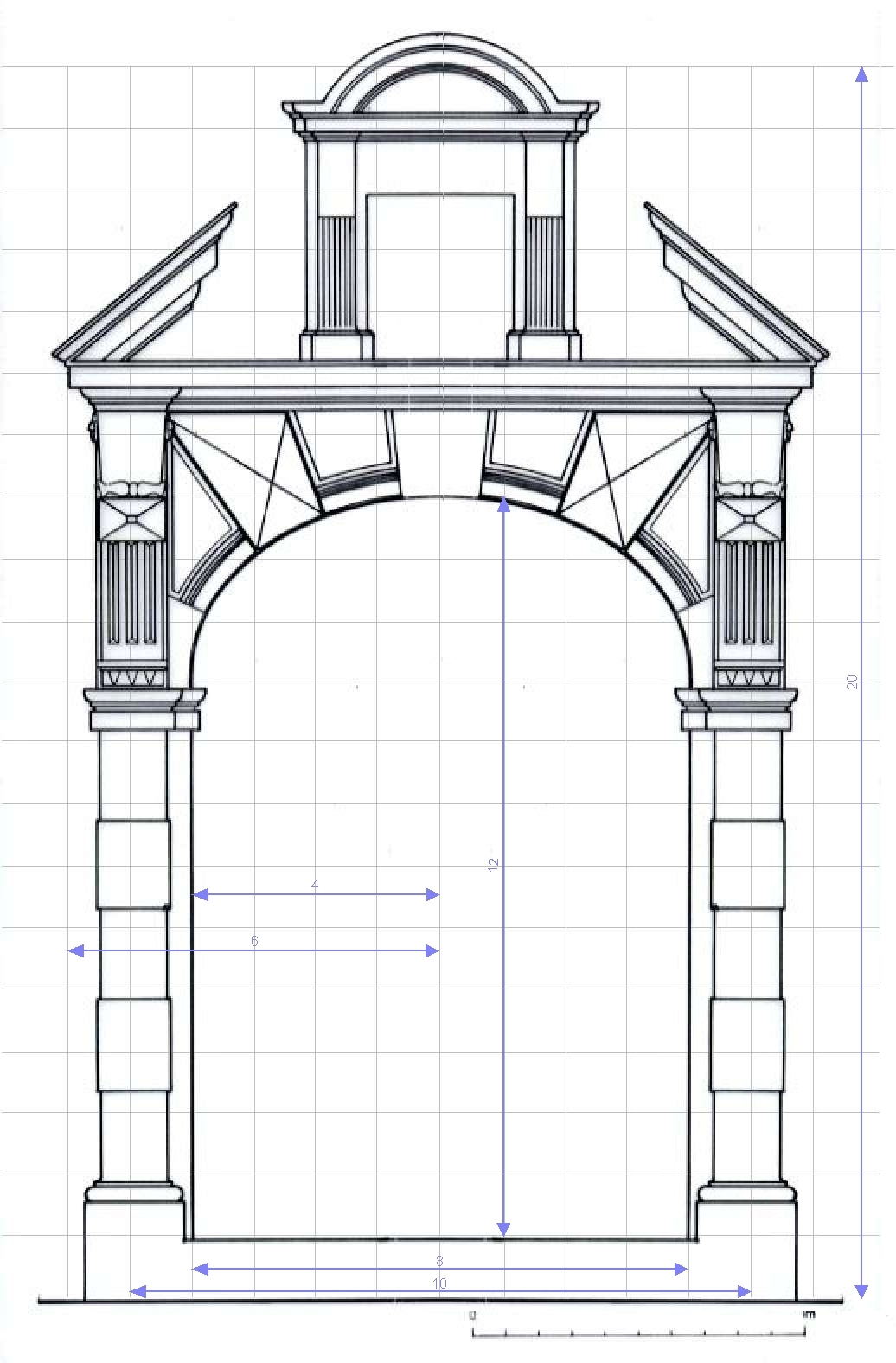 |
Rapport largeur sur hauteur de la baie : 8/12mo = 2/3 = quinte, entraxe/Hauteur totale : proche de 10/20 = diapason, arc en anse de panier : petit diamètre/grand diamètre = 6/8 = ¾ = quarte. Nous retrouvons les mêmes rapports arithmétiques, les mêmes accords musicaux, octave, quinte, quarte que dans les portes précédentes ainsi que la moyenne arithmétique : 8/10/12 ( le moyen terme dépasse le premier d’une quantité égale à celle dont il est dépassé ou b=(a+c)/2 ), et la moyenne harmonique : 6/8/12 ( a/b/c soit (b-a)/a = (c-b)/c ).
(1) Au concile de Florence, Grecs et Latins proclamèrent en 1439 l’union des deux églises face à la menace turque. c’est l’époque à partir de laquelle Cosme de Médicis (┼ 1464) va favoriser le renouveau de l’hellénisme en demandant à l’Argyropoulos la traduction des œuvres d’Aristote et au jeune Ficin de traduire Platon. Suite à la querelle qui oppose les partisans de Platon conduits par le cardinal Bessarion aux aristotéliciens et au départ de l’Argyropoulos, Florence tombe aux mains des platoniciens (1471). « l’accord musical est pour ainsi dire vivant, il est rationnel, efficace, il est ce qu’il y a de plus semblable, de plus agréable à l’âme, constitutif des choses,il les maintient, il les meut ; aussi notre Platon a-t–il surtout décrit l’âme qui active, maintient et meut toutes les choses de la nature comme constituées par des nombres et des rapports musicaux, et non pas par de valeurs mathématiques fortuites, comme on le prétend indûment, mais par leurs rapports métaphysiques. » M. Ficin, Compendium in Timaeum, ch. 28, cité par A. Chastel, Marsile Ficin et l’art.
(2) « Mais, si l’on a que deux choses, il est impossible de les combiner convenablement sans une troisième ; car il faut qu’il y ait entre les deux un lien qui les unisse. Or de tous les liens, le meilleur est celui qui de lui-même et des choses qu’il unit, forme une unité aussi parfaite que possible, et cette unité, c’est la proportion qui est de nature à le réaliser complètement. » Timée/31b, traduction E.Chambry, Garnier Flammarion.
(3 Nous devons à Boeckh d’avoir résolu l’énigme de l’âme du monde au 19°siècle. Rivaud, parmi d’autres, en donne une interprétation complète (Timée/35c-36b, traduction de Rivaud, Les Belles-Lettres, association Guillaume Budé, 1925), condensée ici en quelques schémas (consulter aussi les notes qui accompagnent une traduction récente de Luc Brisson).
La première division du mélange consiste en l’imbrication de deux suites géométriques, l’une de raison 2 (intervalles doubles) soit 1 : 2 : 4 : 8, l’autre de raison 3 (intervalles triples) 1 : 3 : 9 : 27.(Les notations 1 : 2 : 3 : 4 et 1/2/3/4 sont équivalentes)
Dans chacune de ces deux suites, les intervalles sont remplis par deux médiétés : la première est la moyenne harmonique entre les deux extrêmes (elle « surpasse les extrêmes ou est surpassée par eux d’une même fraction de chacun d’eux« ) la seconde est la moyenne arithmétique ( la médiété « surpasse les extrêmes d’une quantité égale à celle dont elle est elle-même surpassée« ).
Suite des intervalles doubles :
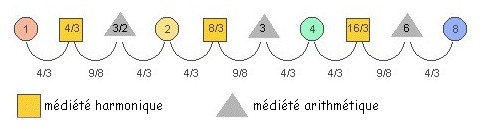
Entre la médiété arithmétique et la médiété harmonique le rapport est de 1+1/8 ou 9/8 (3/2 étant les 9/8 de 4/3). 3 est aussi les 9/8 de 8/3, 6 les 9/8 de 16/3. Les autres rapports sont de 1+1/3 ou 4/3
Suite des intervalles triples :
Les rapports entre moyens et entre moyens et extrêmes sont ici de 4/3 ou de 3/2 (1+1/2).
« De ces relations naissent dans les intervalles ci-dessus désignés, des intervalles nouveaux de un plus un demi, un plus un tiers, un plus un huitième« . 3/2, 4/3, 9/8, nous retrouvons dans les deux suites les fameux rapports de longueur de cordes qui donnent la gamme de Pythagore : la quinte (3/2 ou ratio sesquialtera), la quarte (4/3 ou ratio sesquitertia), le ton (1+1/8 ou ratio sesquioctava en latin) et le demi-ton pythagoricien.
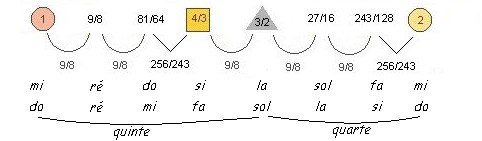
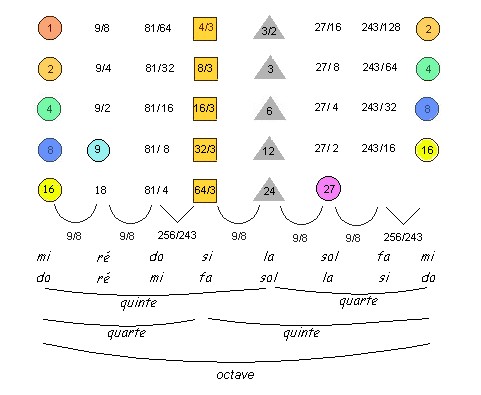
« A l’aide de l’intervalle de 1+1/8, le Dieu a comblé tous les intervalles de 1+1/3, laissant subsister de chacun d’eux une fraction telle que l’intervalle restant fût défini par le rapport du nombre deux cent cinquante-six au nombre deux cent quarante trois. » Effectivement, les rapports de 9/8 ne pouvant combler la totalité des intervalles, Platon est tenu de recourir à deux « leimmas » ou demi-tons pythagoriciens, deux rapports de 256/243. Les longueurs de cordes 1, 9/8, 81/64, 4/3, 3/2, 27/16, 243/128, 2 ainsi obtenues pour le premier intervalle de la division primitive,donnent les intervalles du mode dorien exprimés en ordre descendant : mi, ré, do, si, la, sol, fa, mi, soit cinq tons et deux demi-tons de do à si et de fa à mi. (Les intervalles de cette gamme sont identiques à ceux de la gamme diatonique majeure montante, forme moderne de la gamme de Pythagore, dans laquelle les nombres ne désignent plus des rapports de longueur de corde mais des rapports de fréquence.)
L’ensemble donne une échelle musicale couvrant quatre octaves et une sixte. Les sept nombres retenus par Platon correspondent au rayon de l’orbite de chacune des sept planètes qui pour les Anciens tournent autour de la terre, la distance terre-lune étant égale à 1. L’âme du monde a donc une structure mathématique et musicale qui se révèle à nous dans la nature et particulièrement dans le modèle des astres, cosmos « harmonisé » par les proportions qui lui confèrent sa perfection et sa beauté.
(4) Lettre d’Alberti à Matteo de’ Pasti, 14 novembre 1454. NY, Pierpont Morgan Library, reproduite p.97 dans « Leon Battista Alberti, opera completa » Franco Borsi, Electa, Milan, 1973
(5) Francesco Giorgi’s Memorandum for Francesco della Vigna in « Architectural Principles », Rudolf Wittkower, annexe 1. Francesco Giorgi ou Zorzi, moine franciscain du monastère rattaché à l’église est proche du courant de la Cabale chrétienne animé par Pic de la Mirandole. F. Giorgiest l’auteur d’un ouvrage De harmonia totius, édité à Venise en 1525 qui tente de concilier catholicisme et pensée néo-platonicienne et qui eut une influence non négligeable en France puisque qu’elle fut éditée à Paris en1545 et traduite en français par Le Fèvre de la Boderie, adversaire résolu du protestantisme, en 1579.