L’architecture selon Vitruve
Située dans la cour intérieure du n° 19 de la rue Bazoges, la porte se trouve dans un corps de bâtiments, faisant partie de l’ancien hotel d’Huré, où furent menés des travaux en 1516, à l’initiative du maire Jehan Conan, afin améliorer l’état sanitaire des locaux destinés aux grandes escholles publiques (1)1. Une génération plus tard, la municipalité instaure un véritable monopole en interdisant à tous manants et habitants de cette ville d’envoyer leurs enfants à d’autres écoles qu’és grandes escholles publiques . Trois disciplines y étaient enseignées, aux fils de notables : rhétorique dialectique, poésie et langue grecque, langue latine. (2)
Cette porte présente une ordonnance antiquisante, ses moulures sont soignées : pilastres cannelés (cannelures à listels et rudentures dans la partie basse) sur base, chapiteaux doriques (astragale, gorgerin nu, échine en quart de rond, tailloir). Un entablement composé d’une architrave monolithique à trois fasces d’une même hauteur, d’une frise bombée interrompue, comme la base du fronton triangulaire qu’elle supporte. Interruption qui laisse place au blason sculpté des Durand de la Vaux-Martin : « De gueule, à trois étoiles d’or en devise, et un soleil d’or en abîme ». A noter : le mouvement giratoire suggéré par la présentation des deux cuirasses, la droite de face, la gauche de dos, circularité soulignée par le profil des boucliers, le mouvement des étendards et l’enroulement des rinceaux du heaume. Une telle composition n’est pas le fruit d’une élémentaire pratique artisanale.
L’ensemble est difficile à dater. Des Durand de la Vaux-Martin sont connus pour avoir été officiers du Présidial au XII°. Il est possible que cette porte ne fut pas telle quelle, celle des Grandes Ecoles, établissement qui ferma à l’ouverture du Collège Jeanne d’Albret (1565) (4). La particularité d’associer chapiteaux doriques et architrave ionique (si on se réfère aux cinq ordres de Serlio) au lieu du couple chapiteau dorique et frise à métope-triglyphes, se retrouve dans plusieurs élévations locales fin XVI °, début XVII° (3)
Vitruve : « en quoi consiste l’architecture »
Le seul traité d’architecture qui nous soit parvenu de l’antiquité est celui de Vitruve, architecte romain du premier siècle av. JC. L‘ouvrage était connu des érudits médiévaux. Le manuscrit de la bibliothèque de Saint-Gall fut exhumé en 1416. L’imprimerie va permettre au 16 ° siècle sa grande diffusion. Imprimé en latin dès 1486 à Rome, dépourvu de dessins, il est édité à Venise par Fra Giocondo en 1511, accompagné de gravures. Il est traduit en français par Jean Martin et illustré en partie par Jean Goujon en 1547 (5). Edité de très nombreuses fois en latin et langues « vulgaires » européennes le De architectura est la référence incontournable pour la réflexion et la pratique architecturale de la Renaissance, jusqu’à la période classique-baroque, époque à laquelle tout en ne cessant de clamer leur fidélité à l’esprit du texte original, certains traducteurs-commentateurs vont s’écarter des interprétations admises jusque là. C’est le cas particulièrement de Perrault au XVIIème siècle, comme nous verrons plus avant, au sujet de son différent avec Blondel ; Perrault dont la traduction va prolonger la large diffusion du texte antique et tenter d’imposer la lecture « moderne » qu’il en fait.
Des qualités de l’architecte
Selon Vitruve, l’architecture, cette « science qui s’acquiert par la pratique et la théorie« , exige toute une palette de compétences et de connaissances. Outre l’ingéniosité et le goût du travail, l’architecte doit avoir « de la facilité pour la rédaction, de l’habileté pour le dessin, des connaissances en géométrie ; il doit avoir quelque teinture de l’optique, posséder à fond l’arithmétique, être versé dans l’histoire, s’être livré avec attention à l’étude de la philosophie, connaître la musique, n’être point étranger à la médecine, à la jurisprudence, être au courant de la science astronomique qui nous initie aux mouvements du ciel » Liv.I, chap.1 (6). Notons ses arguments à propos de la maîtrise des mathématiques : « La géométrie offre plusieurs ressources à l’architecte : elle le familiarise avec la régle et le compas, qui lui servent surtout à déterminer l’emplacement des édifices, et des alignements à l’équerre, au niveau et au cordeau… A l’aide de l’arithmétique, on fait le total des dépenses, on simplifie le calcul des mesures, on règle les proportions qu’il est difficile de trouver par les procédés que fournit la géométrie« (6). La musique est elle aussi indispensable : « afin que l’on saisisse bien la proportion canonique et mathématique et que l’on tende convenablement les balistes… », un même son garantissant une même tension des cordes à boyau nécessaire pour lancer les projectiles bien « droit ». « La musique est encore nécessaire pour les théâtres où des vases d’airain sont placés dans des cellules pratiquées sous les degrés. Les sons différents qu’ils rendent, réglés d’après les proportions mathématiques, selon les lois de la symphonie ou accord musical, répondent, dans leur division exacte, à la quarte, à la quinte et à l’octave, afin que la voix de l’acteur, concordant avec la disposition de ces vases, et graduellement augmentée en venant les frapper, arrive plus claire et plus douce à l’oreille du spectateur« (6).
Les cinq points fondamentaux de l’architecture ?
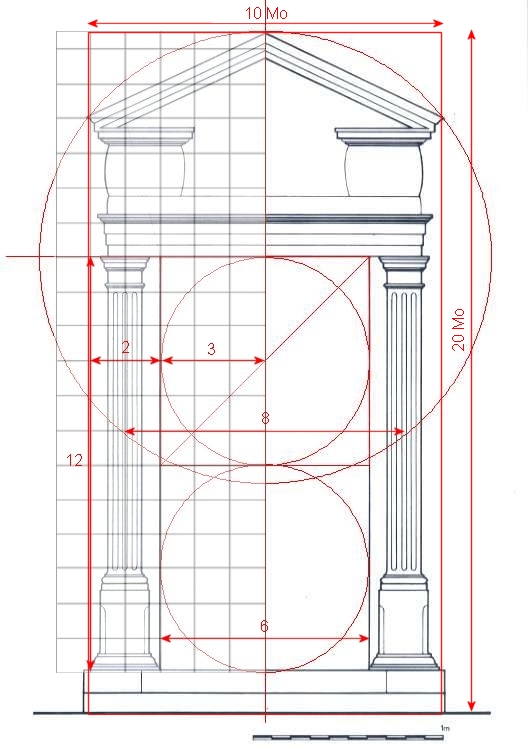
Elle a pour objet : l’ordonnance, la disposition, l’eurythmie engendrée par la « symmetria« (7) ou proportion, la convenance et la distribution
Définissons succintement cinq de ces points : l’ordonnance désigne l’aménagement correct des parties intérieures d’un édifice et la conformité de ses proportions générales avec la « symmetria » laquelle se règle sur le module, mesure déterminée d’après laquelle on établit les dimensions de l’ensemble de l’ouvrage et de chacune de ses parties.
» La disposition est la situation avantageuse des différentes parties, leur grandeur appropriée aux usages auxquels ils sont destinés... »
» La bienséance est la convenance des formes extérieures d’un édifice dont la construction bien entendue donne l’idée de sa destination... La distribution étant le choix avantageux des matériaux et de l’emplacement où on doit les mettre en œuvre »
« L’eurythmie est l’heureuse harmonie des différentes parties de l’édifice… lorsque la hauteur répond à la largeur, la largeur à la longueur et l’ensemble aux lois de la « symmetria« . Cette symmetria, Vitruve la définit comme » la proportion qui règne entre toutes les parties de l’édifice, et le rapport de ces parties séparées avec l’ensemble, à cause de l’uniformité des mesures. Dans le corps humain, le coude, le pied, la main, le doigt et les autres membres, offrent des rapports de grandeur ; ces mêmes rapports doivent se rencontrer dans toutes les parties d’un ouvrage. Pour les édifices sacrés, par exemple, c’est le diamètre des colonnes ou un triglyphe qui sert de module… » (8) La symmetria, n’est pas à confondre avec notre symétrie axiale, elle est la proportion qui règle toutes les parties de l’édifice entre elles et avec l’ensemble, à cause de l’uniformité des mesures.
Le corps humain comme modèle de proportion
Dans le premier chapitre de son troisième livre intitulé « De l’ordonnance du bastiment des temples, et de leurs proportions avec la mesure du corps humain », Vitruve précise sa pensée (9) : « Pour bien ordonner un Edifice il faut avoir égard à la Proportion (Symmetria) qui est une chose que les architectes doivent sur tout observer exactement. Or la Proportion dépend du rapport (proportio) que les Grecs appellent Analogie. Car rapport est la convenance de mesure (commodulation) qui se trouve entre une certaine partie des membres & le reste de tout le corps de l’ouvrage, par laquelle toutes les proporions sont réglées. Car jamais un bastiment ne pourra estre bien ordonné s’il n’a cette proportion & ce rapport, & si toutes les parties ne sont à l’égard les unes des autres ce que celles du corps d’un homme bien formé sont, estant comparées ensemble ». Dans le corps humain, nous dit Vitruve, le coude, le pied, la main, le doigt et les autres membres offrent des rapports de grandeur ; ces mêmes rapports doivent se rencontrer dans toutes les parties d’un ouvrage. Pour les édifices sacrés, par exemple, c’est le diamètre des colonnes ou la largeur d’un triglyphe qui sert de module.« Pour bien ordonner un édifice, il faut avoir égard à la symmetria ( ou proportion ) qui est une chose que les architectes doivent sur tout observer exactement… »
On peut s’étonner que Vitruve propose ainsi comme modèle de proportion le corps de l’homme. Pourtant nous apprenons de Platon (mentionné plusieurs fois par Vitruve), dans le Timée (42b), que le Démiurge, après avoir créé le cosmos et les animaux divins, confia à ces « jeunes dieux le soin de façonner des corps mortels, de compléter leur œuvre en ajoutant tout ce qu’il fallait encore ajouter à l’âme humaine et tous les accessoires qu’elle exigeait, puis de commander et de gouverner aussi sagement et aussi bien qu’ils le pourraient cet être mortel, à moins qu’il ne fût lui-même cause de son malheur » (E. Chambry trad.). L’homme, partie intégrante de ce monde ordonné, est un élément en réduction de ce cosmos, un microcosme. Les proportions de son corps, son harmonie, sont une des manifestations de cette « symmétrie » cosmique.
Traduction partielle du texte de Vinci en écriture spéculaire « Vitruve dit, dans son ouvrage sur l'architecture : la Nature a distribué les mesures du corps humain comme ceci :Quatre doigts font une paume, et quatre paumes font un pied, six paumes font un coude : quatre coudes font la hauteur d’un homme. Et quatre coudes font un double pas, et vingt-quatre paumes font un homme ; et il a utilisé ces mesures dans ses constructions ». Deux exemples, parmi beaucoup d'autres, de recours au module pour déterminer la proportion des éléments : un portique dorique, selon Vignole (1562, ouvrage très répandu, version du XVII° présente à la médiathèque de La Rochelle). Autre exemple : Une porte et sa grille modulaire selon Philibert de l'Orme . modules : Vignole et Philibert de l’Orme
Notions de proportions : Il convient de ne pas confondre rapport et proportion :
|
Euclide : » Le rapport est la relation qualitative en ce qui concerne la dimension entre deux grandeurs homogènes. La proportion est l’équivalence des rapports « . Le rapport est le quotient de deux grandeurs exprimées selon une même grandeur de référence, l’unité ou le module en architecture qui peut correspondre par exemple au diamètre ou demi-diamètre d’une colonne : 1/2, 3/4, a/b La proportion ne désigne pas, comme dans le langage courant, un simple rapport comme la longueur d’une salle comparée à sa largeur, mais bien l’égalité de rapports. Dans la proportion a/b = c/d, a et d sont les termes extrêmes, b et c , les moyens. La proportion est dite continue si b=c, ce qui donne une relation entre trois grandeurs, deux extrêmes et une moyenne : a/b = b/c. Les Anciens désignaient comme médiété, indifféremment, soit le terme moyen soit la moyenne elle-même. Il distinguèrent principalement trois types de proportions : la géométrique, l’arithmétique, l’harmonique . Selon Matila C. Ghyka, ( » le nombre d’or « ), Matila C. Ghyka, Gallimard, 1931.P.32elles auraient été transmises à Platon par les Pythagoriciens de Syracuse, lors de son premier voyage en Sicile. Ces proportions, combinaison de deux ou plusieurs relations, n’impliquent pas nécessairement l’égalité de fractions, elles peuvent aussi bien s’exprimer par l’égalité de différences ou d’autres formes de comparaison. Ainsi dans la moyenne géométrique le plus grand terme (c) est au moyen (b) ce que le moyen est au plus petit (a) ; elle peut s’exprimer sous les formes suivantes : c-b/b-a = c/b ou a/b = b/c ou b² = ac ou b = V¯ac. Les Grecs écrivaient une proportion généralement sous la forme d’une série (ou progression) : 1, 2, 4 ou 3, 9, 27 pour désigner une progression géométrique de raison 2 (carrée) ou 3 (cubique) (2). Dans la moyenne arithmétique, le moyen terme dépasse le premier d’une quantité égale à celle dont il est lui-même dépassé, soit c-b = b-a ou b = (a+c)/2 comme la progression arithmétique 1, 2, 3 (de raison 1) ou 5, 7, 9 (de raison 2). La moyenne harmonique (b) entre deux extrêmes (a et c) dépasse le plus petit terme (a) et est surpassée par le plus grand (c) » de la même fraction de chacun d’eux » (Platon) soit (b-a)/a = (c-b)/c Piero Della Francesca dans son traité de perspective (De prospectiva pingendi, traduit et annoté par Jean-Pierre Le Goff, édition In Media Res, Paris 1998) compare des produits : »…elles sont proportionnelles entre elles, par le fait que le rapport du produit de AE par AL à celui de EI par EF est comme le rapport du produit de LI par LN à celui de IP par IQ« . Il parle de proportion double comme l’est 2-4-8 (de raison 2), sesquialtère comme 4-6-9 (de raison 3/2), sesquitierce comme 9-12-16 (de raison 4/3), particulièrement remarquables parmi les » innombrables » proportions [ I, 11 ] La progression arithmétique des quatre premiers nombres, la tetractys, 1, 2, 3, 4 attira particulièrement l’attention des Pythagoriciens. Leur somme, 10, est un nombre symbolique de l’univers signalé par Vitruve lui-même. Leurs rapports, comme nous le verrons plus avant correspondent aux longueurs de cordes qui produisent les principaux accords musicaux : l’octave , la quinte et la quarte.
|
Commodulation de la porte de la rue Bazoges.
1) En 1541, François premier érige par lettres patentes les écoles publiques en collège avec un Principal et plusieurs régents laïques. Selon Jourdan(Les éphémérides, p28) : contrat passé entre la ville et maître Guillaume le 6 février 1545 pour l’achat de deux maisons contiguës pour en faire les Grandes écoles publiques. cf Jean Flouret, « Cinq siècles d’enseignement secondaire à La Rochelle (1504-1972)… » La Rochelle Quartier Latin 1973.
2) Jourdan : 19 juillet 1560:Rodolphe de Guillemelle est nommé principal régent des écoles publiques. Sous son autorité trois autres régents
3) château de Laleu, Saint-Martin de Ré : hôtel Clerjotte, porte n° 13 rue du général Lapasset, porte cour intérieure de la maison Nicolas Venette , porte des échevins… Ce qui montre que les cinq ordres définis notamment par Serlio ne font pas encore autorité.
4) Amos Barbot (Archives historiques de la Saintonge et de l’Aunis, 1887) p.230 : »… et pour faire les dits deniers, furent décrétés et vendus par ledit sieur maire… la petite maison des grandes escholles qui fait le coing tournant en la rue de Bazauges, … »
(5) Pour les éditions et commentaires : Françoise Fichet, ouvrage cité, p.56
(6) pour plus de précision consulter « L’architecture de Vitruve » nouvelle traduction, en regard du texte latin, de Ch-L Maufras (1847), » De l’architecture ; qualités de l’architecte » p.27à 43 « en quoi consiste l’architecture », p43 à 51, disponible sur le serveur de la BNF (gallica.bnf.fr/ark:/12148/bpt6k236629 )
(7) Nous choisissons ce terme pour le distinguer de l’acception actuelle de symétrie.
(8) Rappelons que ce concept de « symmetria » désigne une proportion de raison x qui peut être arithmétique, harmonique ou géométrique, proportion dans laquelle les grandeurs sont exprimées par rapport à une grandeur de référence, le module. Le mot commodulatio est aussi employé comme synonyme, on le retrouve chez Alberti, il n’est guère moins latin, nous dit Perrault dans une de ses notes, que celui de commensus dont use Cicéron.
(9) Nous choisissons cette fois la traduction de Perrault. Accompagnée d’une illustration elle nous semble plus explicite tout en suggérant la difficulté de traduction d’un texte qui présente de nombreuses obscurités.